Tideman - CS50x 2023
通过这个程序,你将实现一个Tideman选举的算法,例子如下:
$ ./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob
Charlie
背景
你已经了解了简单多数选举,它遵循一个非常简单的算法来确定选举的获胜者:每个选民都有一票,并且获得最多票数的候选人获胜。
但是简单多数投票确实有一些缺点。例如,如果在有三名候选人的选举中,投了以下选票,会发生什么情况?
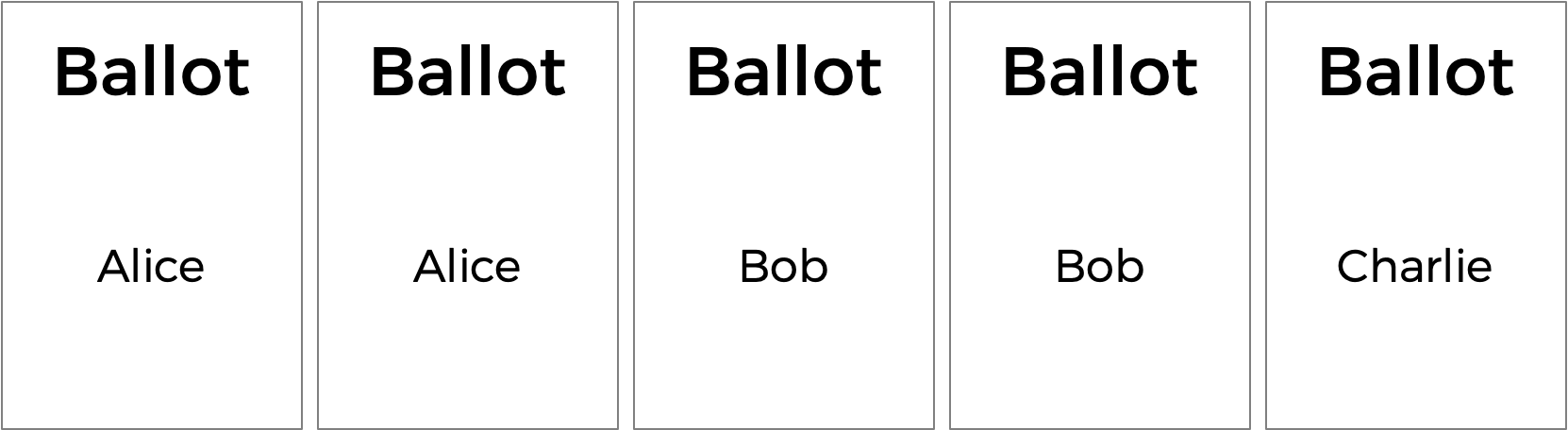
简单多数投票会宣布 Alice 和 Bob 之间平局,因为每个人都有两票。但这样算合理吗?
还有另一种投票系统,称为排序复选制。在排序复选制中,选民可以投票给多名候选人。他们不仅可以投票给他们的首选,还可以按偏好顺序对候选人进行排名。因此,由此产生的选票可能如下所示。
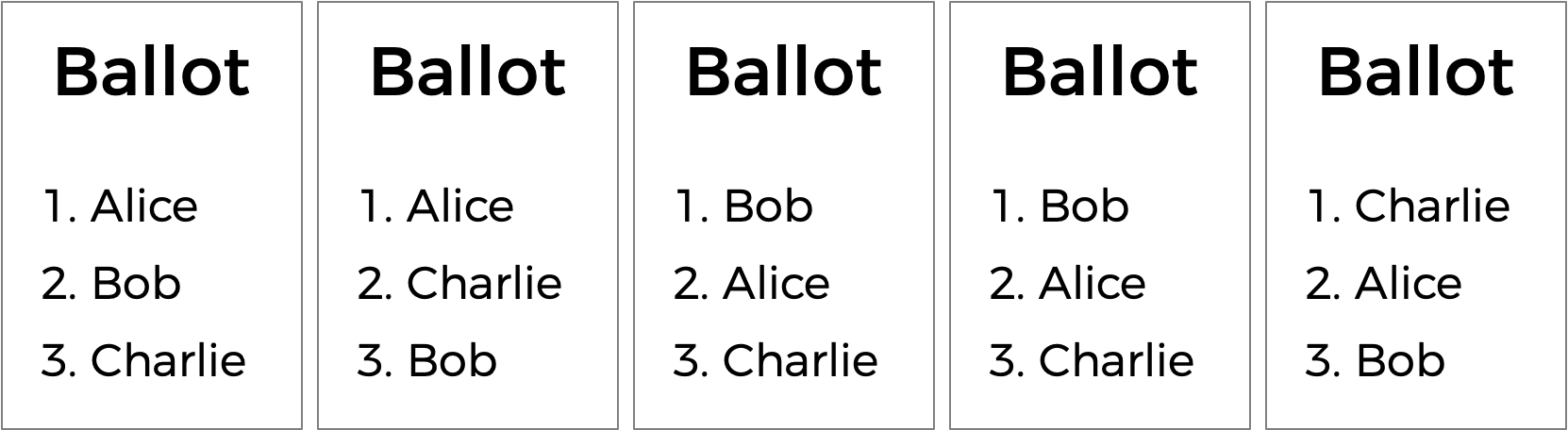
在这里,除了指定他们的首选候选人之外,每位选民还指出了他们的第二和第三选择。最初,Alice和Bob的得票数相同,呈平局状态。但是选择 Charlie 的选民更喜欢 Alice 而不是 Bob,因此 Alice 可以在这里被宣布为获胜者。
排序选择投票还可以解决简单多数投票的另一个潜在缺点。看看下面的选票。
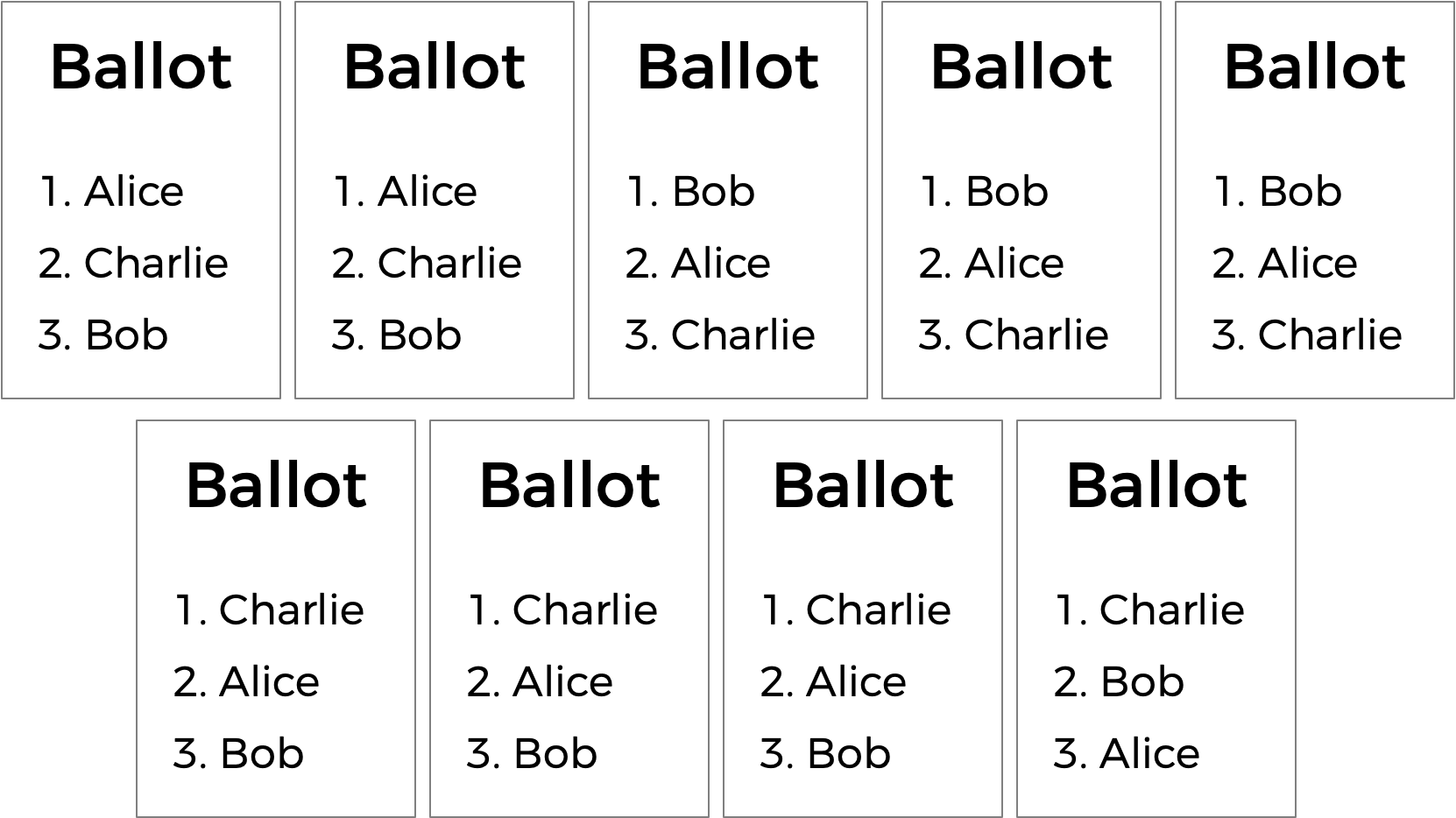
谁应该赢得这次选举?在简单多数投票中,每个选民只选择他们的首选,Charlie 以四票赢得这次选举,而 Bob 只有三票,Alice 只有两票。(请注意,如果您熟悉立即决胜投票系统,那么 Charlie 也会在该系统下获胜)。然而,Alice 可能会合理地认为她应该成为选举的获胜者,而不是 Charlie:毕竟,在九名选民中,大多数人(五人)更喜欢 Alice 而不是 Charlie,因此,比起Charlie获胜,大多数人更乐于见到Alice获胜。
Alice 在这次选举中是所谓的“孔多塞获胜者 (Condorcet winner)”:即在与另一位候选人的任何一对一比赛中获胜的人。如果选举只有 Alice 和 Bob,或者只有 Alice 和 Charlie,Alice 都会获胜。
Tideman 投票方法(也称为“排序对”)是一种排序选择投票方法,保证在存在孔多塞获胜者的情况下产生选举的孔多塞获胜者。
一般来说,Tideman 方法通过构建候选人的“图”来工作,其中从候选人 A 到候选人 B 的箭头(即边)表示候选人 A 在与候选人 B 的一对一比赛中获胜。那么,对于上述选举,图示会是这样:
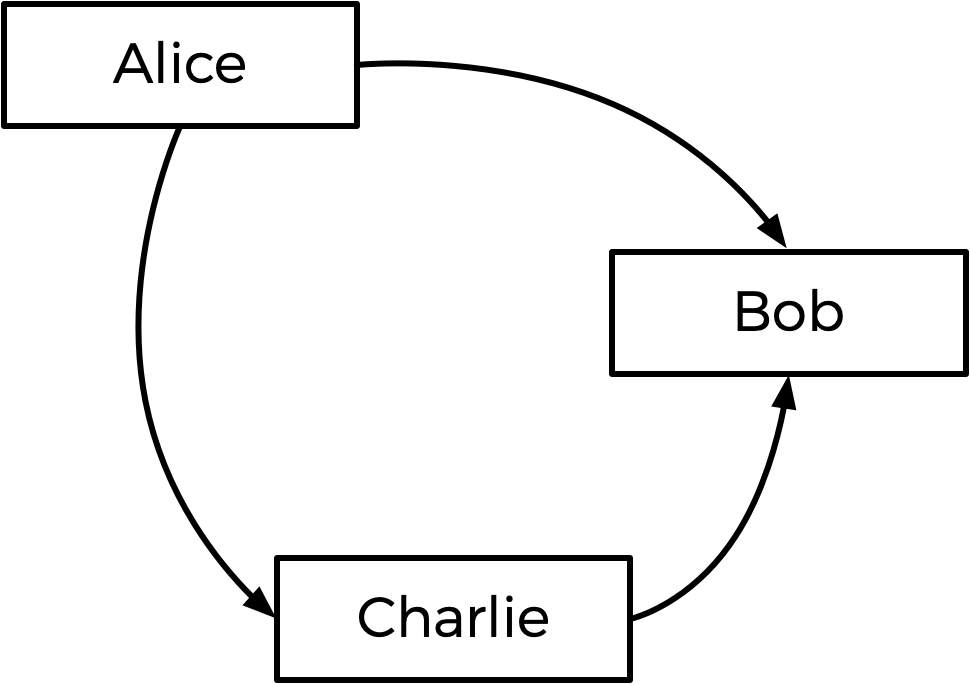
Alice指向Bob的箭头表示更多选民偏好Alice胜过Bob (5人选Alice, 4人选Bob)。同样,其他箭头表示更多选民喜欢 Alice 而不是 Charlie,更多选民喜欢 Charlie 而不是 Bob。 根据这张图,Tideman方法认为选举的获胜者应该是图的“源点”(也就是没有箭头指向的候选人)。 在这种情况下,“源点”是Alice——她是唯一一个没有箭头指向的候选人,这意味着在两两对决中,没有人比Alice更受选民青睐。因此,Alice被宣布为本次选举的获胜者。
然而,也可能出现一种情况:在绘制箭头之后,不存在孔多塞获胜者。 考虑以下选票。

在Alice和Bob之间,Alice以7比2的优势胜过Bob。 在Bob和Charlie之间,Bob以5比4的优势胜过Charlie。 但是在Charlie和Alice之间,Charlie以6比3的优势胜过Alice。 如果我们把这张图画出来,就会发现没有“源点”! 我们有一个候选人循环,Alice击败Bob,Bob击败Charlie,Charlie击败Alice(很像石头剪刀布游戏)。 在这种情况下,似乎没有办法选出获胜者。
为了解决这个问题,Tideman算法必须小心避免在候选人图中创建循环。 它是如何做到的呢? 该算法首先锁定最强的边,因为这些边可以说是最重要的。 具体来说,Tideman算法规定,应该根据对决的“强度”(即,有多少选民更偏爱某个候选人胜过其对手,偏爱的人数越多,强度就越高)逐一地将对决的边“锁定”到图中。 只要边可以被锁定到图中而不产生循环,就添加该边; 否则,忽略该边。
在上述的投票示例中,这个算法会如何运作呢? 首先,在所有候选人两两对决中,Alice击败Bob的优势最大,有7名选民更偏爱Alice而不是Bob(没有其他对决的胜者获得的选民偏爱超过7人)。 因此,Alice-Bob箭头首先被锁定到图中。 接下来,Charlie以6比3击败Alice的优势位居第二,因此这个箭头会被锁定。
但要注意:如果现在添加从Bob到Charlie的箭头,就会形成一个循环! 由于该图不允许出现循环,因此应该跳过这条边,直接忽略。 如果还有其他箭头需要考虑,就继续分析,但因为这是最后一个箭头,所以图的构建就完成了。
此逐步过程如下所示,最终图在右侧。
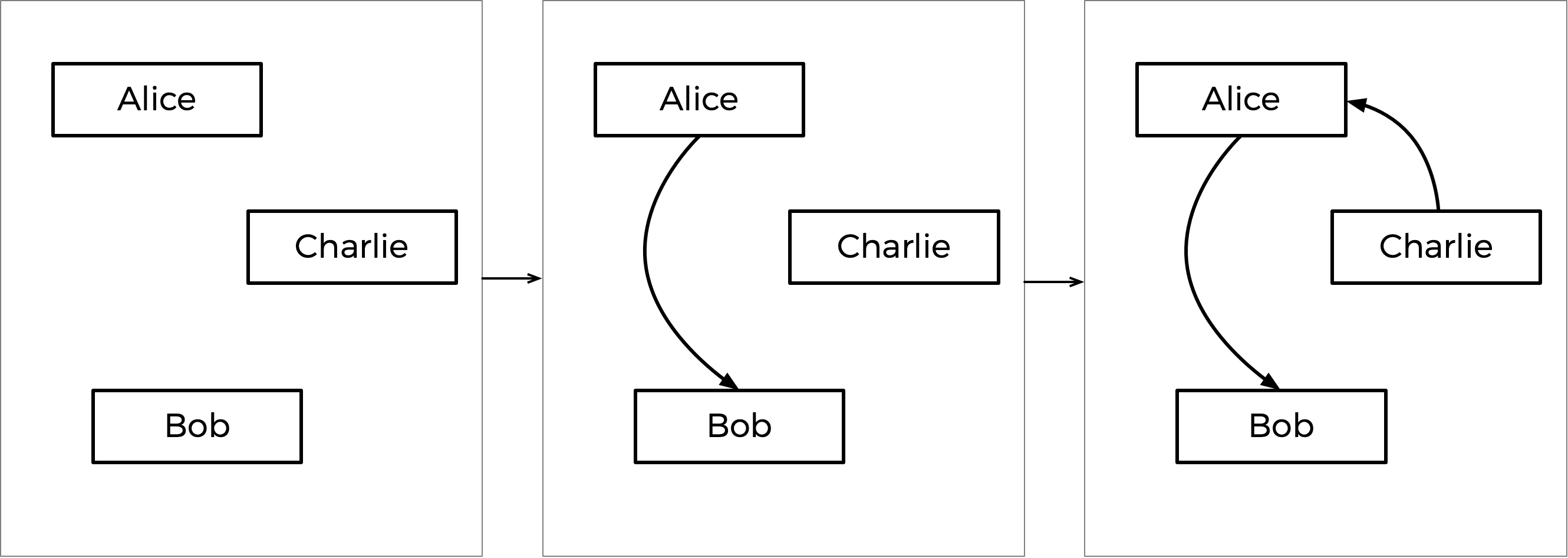
根据最终生成的图,Charlie是“源点”(没有箭头指向他),因此Charlie被宣布为本次选举的获胜者。
更正式地说,Tideman投票方法包括三个部分:
- 统计:在所有选民表达完各自的偏好之后,统计每两位候选人之间的对决情况,确定哪一位更受青睐,以及受青睐的程度。
- 排序:按照胜利的强度,以降序排列候选人对。胜利的强度指的是,有多少选民更偏爱胜出的候选人。
- 锁定:从强度最高的候选人对开始,按顺序逐一检查每一对候选人,如果将这对候选人的胜负关系“锁定”到图中不会形成循环,则执行锁定操作。
一旦图完成,图的“源点”(没有边指向它的那个)就是获胜者!
开始
登录cs50.dev,点击你的终端窗口,然后单独执行cd。 你应该发现你的终端窗口的提示符类似于以下内容:
接下来执行
wget https://cdn.cs50.net/2022/fall/psets/3/tideman.zip
以便将名为tideman.zip的ZIP文件下载到你的代码空间中。
然后执行
以创建一个名为tideman的文件夹。 现在你不再需要这个ZIP文件了,所以可以执行
然后,在提示符后输入 y 并按回车键,删除您下载的 ZIP 文件。
现在输入:
然后按回车键,进入(或打开)该目录。您的命令提示符应该类似下面这样。
如果一切顺利,您应该执行:
就能看到一个名为 tideman.c 的文件。执行 code tideman.c 就会打开该文件,您可以在其中编写代码。如果不是,请回顾您的步骤,看看哪里操作有误!
理解
让我们来看看 tideman.c。
首先,请注意二维数组 preferences(偏好)。整数 preferences[i][j] 表示有多少选民更偏爱候选人 i 而不是 j。
文件中还定义了另一个二维数组 locked,用于表示候选人之间的关系图。因此,如果 locked[i][j] 为 true,则表示候选人 i 指向 j 存在一条边;false 则表示没有边。这种图的表示方法,也称为“邻接矩阵”。
接下来是一个名为 pair 的结构体(struct),用于表示候选人配对关系:每对包含胜者 (winner) 和败者 (loser) 的候选人索引。
候选人本身存储在数组 candidates 中,该数组是一个 string 数组,表示每个候选人的姓名。还有一个 pairs 数组,用于存储选举中所有存在偏好关系的候选人对。
接下来,我们来看 main 函数。请注意,在确定候选人数量后,程序会循环遍历 locked 图,并最初将所有值设置为 false,这意味着初始状态下,图中没有任何边。
接下来,程序通过调用 vote 函数,将选民的偏好信息存储到 ranks 数组中,其中 ranks[i] 是选民的第 i 个偏好的候选人的索引。该函数负责获取这些排名信息,并更新全局变量 preferences。
在所有选票录入完毕后,候选人对将通过调用 add_pairs 添加到 pairs 数组,通过调用 sort_pairs 进行排序,并通过调用 lock_pairs 锁定到图中。最后,调用 print_winner 来打印出选举获胜者的姓名!
在该文件的更下方,您将看到函数 vote、record_preference、add_pairs、sort_pairs、lock_pairs 和 print_winner 都是空白的。请完成这些函数的实现!
规范
完成 tideman.c 的实现,使其模拟 Tideman 选举。
- 完成
vote函数。- 该函数接受
rank、name和ranks这几个参数。如果name与有效候选人的姓名匹配,则应更新ranks数组,记录选民对该候选人的偏好顺位(0为第一偏好,1为第二偏好,以此类推)。 - 请注意,
ranks[i]代表用户第i顺位的偏好。 - 如果成功记录排名,函数返回
true;否则(例如,name不是候选人姓名时)返回false。 - 您可以假设没有两个候选人会同名。
- 该函数接受
- 完成
record_preferences函数。- 该函数对每位选民调用一次,参数为
ranks数组(ranks[i]代表选民的第i顺位偏好,ranks[0]为第一偏好)。 - 该函数应更新全局数组
preferences,记录当前选民的偏好。preferences[i][j]表示偏好候选人i胜过候选人j的选民人数。 - 您可以假设每位选民都会对每位候选人进行排名。
- 该函数对每位选民调用一次,参数为
- 完成
add_pairs函数。- 该函数应将所有存在偏好的候选人对添加到
pairs数组;不应添加平局的候选人对。 - 该函数应更新全局变量
pair_count,使其等于候选人对的数量(这些候选人对存储在pairs[0]到pairs[pair_count - 1]之间,包含边界)。
- 该函数应将所有存在偏好的候选人对添加到
- 完成
sort_pairs函数。- 该函数应按胜利强度降序排列
pairs数组;胜利强度定义为偏好胜出候选人的选民人数。如果多个候选人对的胜利强度相同,则顺序可以任意。
- 该函数应按胜利强度降序排列
- 完成
lock_pairs函数。- 该函数应创建
locked图,并按胜利强度降序添加边,前提是添加该边不会形成环路。
- 该函数应创建
- 完成
print_winner函数。- 该函数应打印出作为图的源的候选人的姓名。您可以假设不会有多个源。
除了实现 vote、record_preferences、add_pairs、sort_pairs、lock_pairs 和 print_winner 函数(以及根据需要包含其他头文件)之外,不应修改 tideman.c 中的其他部分。 允许向 tideman.c 添加其他函数,但不得更改现有函数的声明。
演练
用法
您的程序应按照以下示例运行:
./tideman Alice Bob Charlie
Number of voters: 5
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Alice
Rank 2: Charlie
Rank 3: Bob
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Bob
Rank 2: Charlie
Rank 3: Alice
Rank 1: Charlie
Rank 2: Alice
Rank 3: Bob
Charlie
测试
请务必测试代码,确保其能处理...
- 具有任意数量候选人的选举(最多
MAX为9) - 按姓名投票给候选人
- 无效选票(例如,投票给不存在的候选人)
- 打印选举的获胜者
执行以下命令以使用 check50 评估代码的正确性。 但请务必自己编译并测试它!
check50 cs50/problems/2023/x/tideman
使用以下命令,通过 style50 检查您的代码风格。
如何提交
在您的终端中,执行以下命令来提交您的代码。
submit50 cs50/problems/2023/x/tideman